Algebra, NAP_20333

Question

{{{question}}}

Worked Solution

{{{workedSolution}}}

Variant 0

DifficultyLevel

505

Question

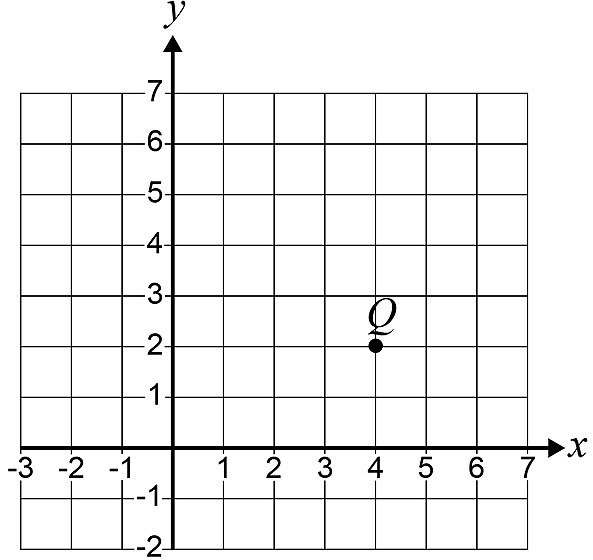
Point QQ is translated down 3 units.



What are the new coordinates of QQ?

Worked Solution

QQ has coordinates ( 4 , 2 )

When translated 3 down, the x\large x-value stays the same and the y\large y-value decreases by 3.

∴\therefore New coordinates are (4 , 2 −- 3 ) = ( 4 , − 1 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $Q$ is translated down 3 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2017/01/NAP-2016-Y7-NC07.png 290 indent3 vpad
What are the new coordinates of $Q$?
workedSolution
$Q$ has coordinates ( 4 , 2 ) When translated 3 down, the $\large x$-value stays the same and the $\large y$-value decreases by 3. $\therefore$ New coordinates are (4 , 2 $-$ 3 ) = {{{correctAnswer}}}.
correctAnswer
( 4 , − 1 )

Answers

Is Correct?Answer
x

( 4 , 5 )

x

( 1 , 2 )

x

( 7 , 2 )

✓

( 4 , − 1 )

Variant 1

DifficultyLevel

507

Question

Point MM is translated to the right 5 units.



What are the new coordinates of MM?

Worked Solution

MM has coordinates ( −- 1 , 2 )

When translated 5 right, the x\large x-value increases by 5 and the y\large y-value stays the same.

∴\therefore New coordinates are ( −- 1 + 5 , 2 ) = ( 4 , 2 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $M$ is translated to the right 5 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v1.svg 300 indent2 vpad
What are the new coordinates of $M$?
workedSolution
$M$ has coordinates ( $-$ 1 , 2 ) When translated 5 right, the $\large x$-value increases by 5 and the $\large y$-value stays the same. $\therefore$ New coordinates are ( $-$ 1 + 5 , 2 ) = {{{correctAnswer}}}.
correctAnswer
( 4 , 2 )

Answers

Is Correct?Answer
✓

( 4 , 2 )

x

( 4 , 6 )

x

( −- 1 , 7 )

x

( 2 , 4 )

Variant 2

DifficultyLevel

509

Question

Point BB is translated left 4 units.



What are the new coordinates of BB?

Worked Solution

QQ has coordinates ( 3 , −- 2 )

When translated 4 left, the x\large x-value decreases by 4 and the y\large y-value stays the same.

∴\therefore New coordinates are ( 3 −- 4 , −- 2) = ( −- 1 , −- 2 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $B$ is translated left 4 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v2.svg 300 indent2 vpad
What are the new coordinates of $B$?
workedSolution
$Q$ has coordinates ( 3 , $-$ 2 ) When translated 4 left, the $\large x$-value decreases by 4 and the $\large y$-value stays the same. $\therefore$ New coordinates are ( 3 $-$ 4 , $-$ 2) = {{{correctAnswer}}}.
correctAnswer
( $-$ 1 , $-$ 2 )

Answers

Is Correct?Answer
x

( −- 2 , −- 1 )

✓

( −- 1 , −- 2 )

x

( −- 6 , 3 )

x

( −- 1 , 3 )

Variant 3

DifficultyLevel

511

Question

Point AA is translated up 5 units.



What are the new coordinates of AA?

Worked Solution

AA has coordinates (−- 2, −- 3 )

When translated 5 up, the x\large x-value stays the same and the y\large y-value increases by 5.

∴\therefore New coordinates are (−- 2, −- 3 + 5 ) = ( −- 2 , 2 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $A$ is translated up 5 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v3.svg 300 indent2 vpad
What are the new coordinates of $A$?
workedSolution
$A$ has coordinates ($-$ 2, $-$ 3 ) When translated 5 up, the $\large x$-value stays the same and the $\large y$-value increases by 5. $\therefore$ New coordinates are ($-$ 2, $-$ 3 + 5 ) = {{{correctAnswer}}}.
correctAnswer
( $-$ 2 , 2 )

Answers

Is Correct?Answer
x

( −- 2 , 1 )

x

( −- 3 , −- 3 )

✓

( −- 2 , 2 )

x

( 1 , −- 2 )

Variant 4

DifficultyLevel

513

Question

Point CC is translated down 3 units and left 2 units.



What are the new coordinates of CC?

Worked Solution

CC has coordinates ( 4 , 2 )

When translated 3 down and 2 left the x\large x-value decreases by 2 and the y\large y-value decreases by 3.

∴\therefore New coordinates are ( 4 −- 2 , 2 −- 3 ) = ( 2 , −- 1 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $C$ is translated down 3 units and left 2 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v4.svg 320 indent2 vpad
What are the new coordinates of $C$?
workedSolution
$C$ has coordinates ( 4 , 2 ) When translated 3 down and 2 left the $\large x$-value decreases by 2 and the $\large y$-value decreases by 3. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v4ws-min.svg 320 indent2 vpad $\therefore$ New coordinates are ( 4 $-$ 2 , 2 $-$ 3 ) = {{{correctAnswer}}}.
correctAnswer
( 2 , $-$ 1 )

Answers

Is Correct?Answer
x

( 4 , −- 1 )

x

( −- 1 , 2 )

✓

( 2 , −- 1 )

x

( 1 , 0 )

Variant 5

DifficultyLevel

515

Question

Point DD is translated right 6 units and down 5 units.



What are the new coordinates of DD?

Worked Solution

DD has coordinates ( −- 2 , 3 )

When translated right 6 and 3 down, the x\large x-value increases by 6 and the y\large y-value decreases by 5.

∴\therefore New coordinates are ( −- 2 + 6 , 3 −- 5 ) = ( 4 , −- 2 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $D$ is translated right 6 units and down 5 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v5.svg 300 indent2 vpad
What are the new coordinates of $D$?
workedSolution
$D$ has coordinates ( $-$ 2 , 3 ) When translated right 6 and 3 down, the $\large x$-value increases by 6 and the $\large y$-value decreases by 5. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v5ws-min.svg 300 indent2 vpad $\therefore$ New coordinates are ( $-$ 2 + 6 , 3 $-$ 5 ) = {{{correctAnswer}}}.
correctAnswer
( 4 , $-$ 2 )

Answers

Is Correct?Answer
✓

( 4 , −- 2 )

x

( 9 , −- 5 )

x

( −- 2 , 4 )

x

( −- 2 , −- 1 )

Variant 6

DifficultyLevel

519

Question

Point WW is translated left 7 units and down 4 units.



What are the new coordinates of WW?

Worked Solution

WW has coordinates ( 4 , 5 )

When translated left 7 and 4 down, the x\large x-value decreases by 7 and the y\large y-value decreases by 4.

∴\therefore New coordinates are ( 4 −- 7 , 5 −- 4 ) = ( −- 3 , 1 ).

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Point $W$ is translated left 7 units and down 4 units.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v6.svg 300 indent2 vpad
What are the new coordinates of $W$?
workedSolution
$W$ has coordinates ( 4 , 5 ) When translated left 7 and 4 down, the $\large x$-value decreases by 7 and the $\large y$-value decreases by 4. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2023/08/Algebra-NAP_20333v6ws-min.svg 300 indent2 vpad $\therefore$ New coordinates are ( 4 $-$ 7 , 5 $-$ 4 ) = {{{correctAnswer}}}.
correctAnswer
( $-$ 3 , 1 )

Answers

Is Correct?Answer
x

( −- 1 , 3 )

✓

( −- 3 , 1 )

x

( 3 , −- 1 )

x

( 1 , −- 3 )

Tags

  • staging_suejones