20298

Question

The rhombus below has a side length d\large d.



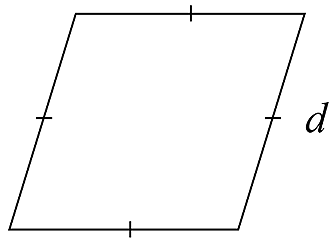
Which expression cannot be used for the perimeter?

Worked Solution

Perimeter = 4d\large d

Options 1, 2 and 4 = 4d\large d

∴\therefore The term not equal to the perimeter = {{{correctAnswer}}}

Variant 0

DifficultyLevel

554

Question

The rhombus below has a side length d\large d.



Which expression cannot be used for the perimeter?

Worked Solution

Perimeter = 4d\large d

Options 1, 2 and 4 = 4d\large d

∴\therefore The term not equal to the perimeter = d\large d ×\times d\large d

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
correctAnswer
$\large d$ $\times$ $\large d$

Answers

Is Correct?Answer
x

2 ×\times (d\large d + d\large d)

x

d\large d ×\times 4

✓

d\large d ×\times d\large d

x

d\large d + d\large d + 2 ×\times d\large d