Algebra, NAPX9-TLD-CA21 v3

Question

A Cartesian plane is shown.



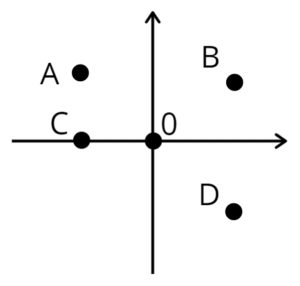
Select the correct statement below.

Worked Solution

{{{correctAnswer}}}

All other statements can be shown to be false.

Variant 0

DifficultyLevel

683

Question

A Cartesian plane is shown.



Select the correct statement below.

Worked Solution

AA is located where  x<\ \large x< 0 and  y>\ \large y> 0.

All other statements can be shown to be false.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
correctAnswer
$A$ is located where $\ \large x<$ 0 and $\ \large y>$ 0.

Answers

Is Correct?Answer
✓

AA is located where  x<\ \large x< 0 and  y>\ \large y> 0.

x

BB is located where  x>\ \large x> 0 and  y<\ \large y< 0.

x

CC is located where  x<\ \large x< 0 and  y<\ \large y< 0.

x

DD is located where  x<\ \large x< 0 and  y=\ \large y= 0.