30101

Question

{{{question}}}

Worked Solution

{{{workedSolution}}}

Variant 0

DifficultyLevel

636

Question

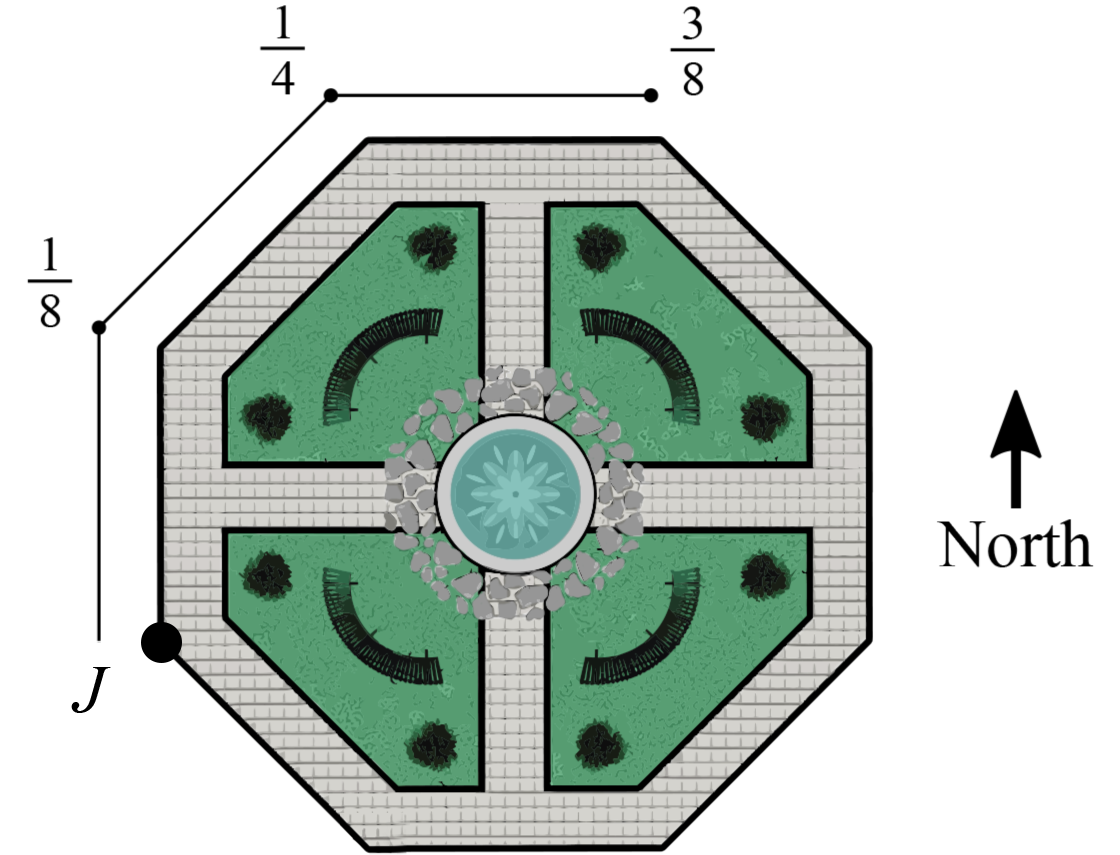
Kramer walks around his local park.

He starts at point JJ and walks east.

If he walks 13\dfrac{1}{3} of the distance around the park, in what direction is he heading?


Worked Solution

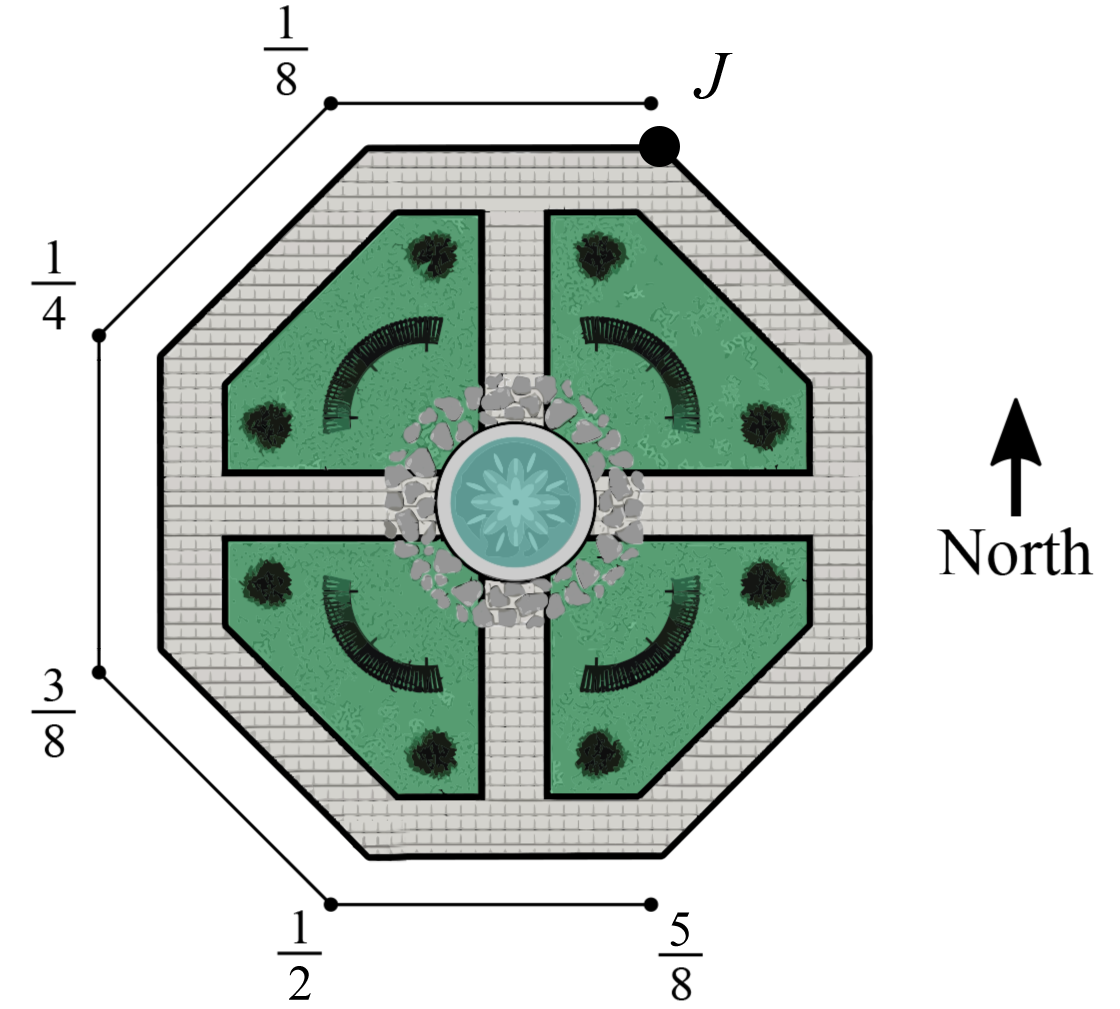
Each edge = 18\dfrac{1}{8} of a full circuit.

Since  14\dfrac{1}{4} < 13\dfrac{1}{3} < 38\dfrac{3}{8}

∴\therefore Kramer is heading north.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Kramer walks around his local park. He starts at point $J$ and walks east. If he walks $\dfrac{1}{3}$ of the distance around the park, in what direction is he heading?
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2018/06/NAPX-E4-CA22.svg 300 indent3 vpad
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2020/09/NAPX-E4-CA22ans.svg 300 indent vpad Each edge = $\dfrac{1}{8}$ of a full circuit. Since  $\dfrac{1}{4}$ < $\dfrac{1}{3}$ < $\dfrac{3}{8}$ $\therefore$ Kramer is heading north.
correctAnswer
north

Answers

Is Correct?Answer
x

east

x

north-east

✓

north

x

north-west

Variant 1

DifficultyLevel

634

Question

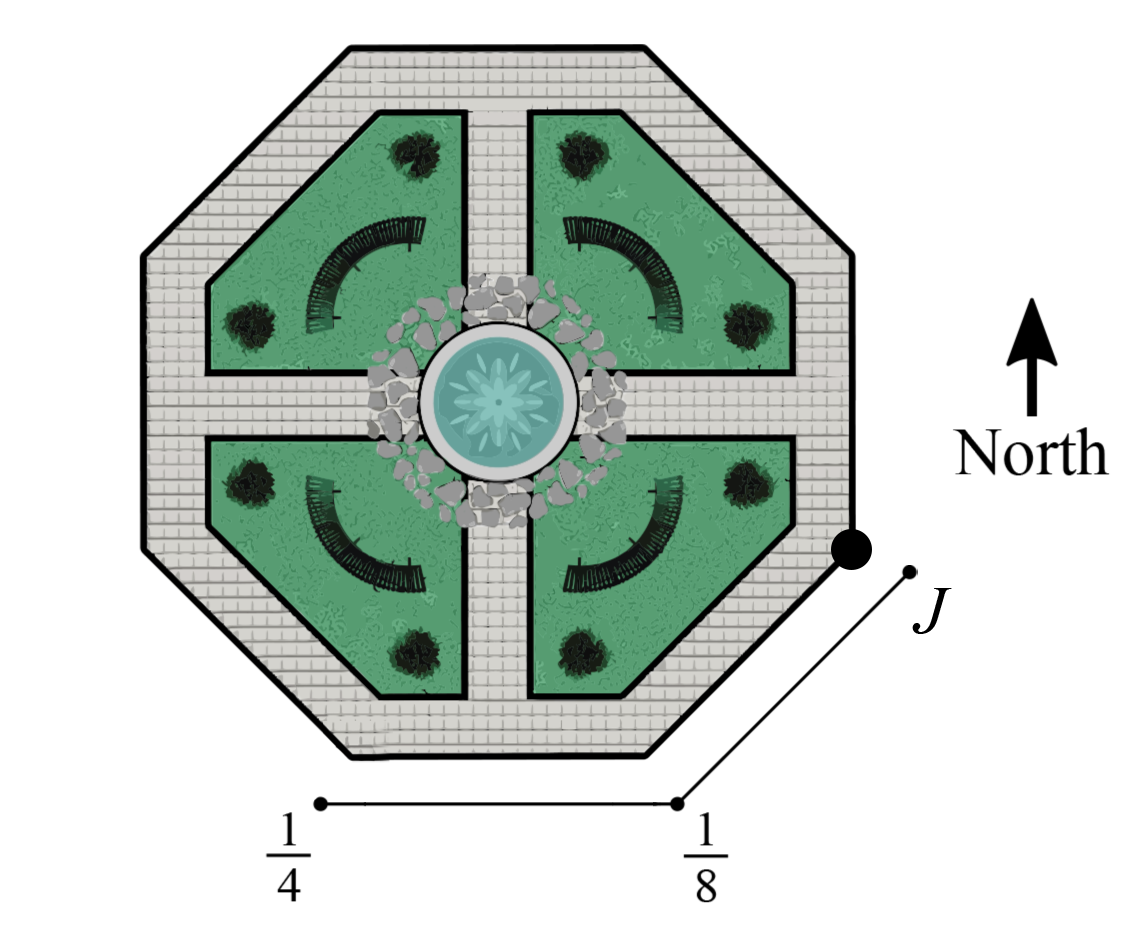
Etienne walks around a section of the gardens of Versailles.

She starts at point JJ and walks north.

If she walks 13\dfrac{1}{3} of the distance around the garden, in what direction is she heading?


Worked Solution

Each edge = 18\dfrac{1}{8} of a full circuit.

Since  14\dfrac{1}{4} < 13\dfrac{1}{3} < 38\dfrac{3}{8}

∴\therefore Etienne is heading east.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Etienne walks around a section of the gardens of Versailles. She starts at point $J$ and walks north. If she walks $\dfrac{1}{3}$ of the distance around the garden, in what direction is she heading?
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-q-var1.png 350 indent3 vpad
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-sol-var1.png 350 indent vpad Each edge = $\dfrac{1}{8}$ of a full circuit. Since  $\dfrac{1}{4}$ < $\dfrac{1}{3}$ < $\dfrac{3}{8}$ $\therefore$ Etienne is heading east.
correctAnswer
east

Answers

Is Correct?Answer
x

north

x

north-east

✓

east

x

south-east

Variant 2

DifficultyLevel

636

Question

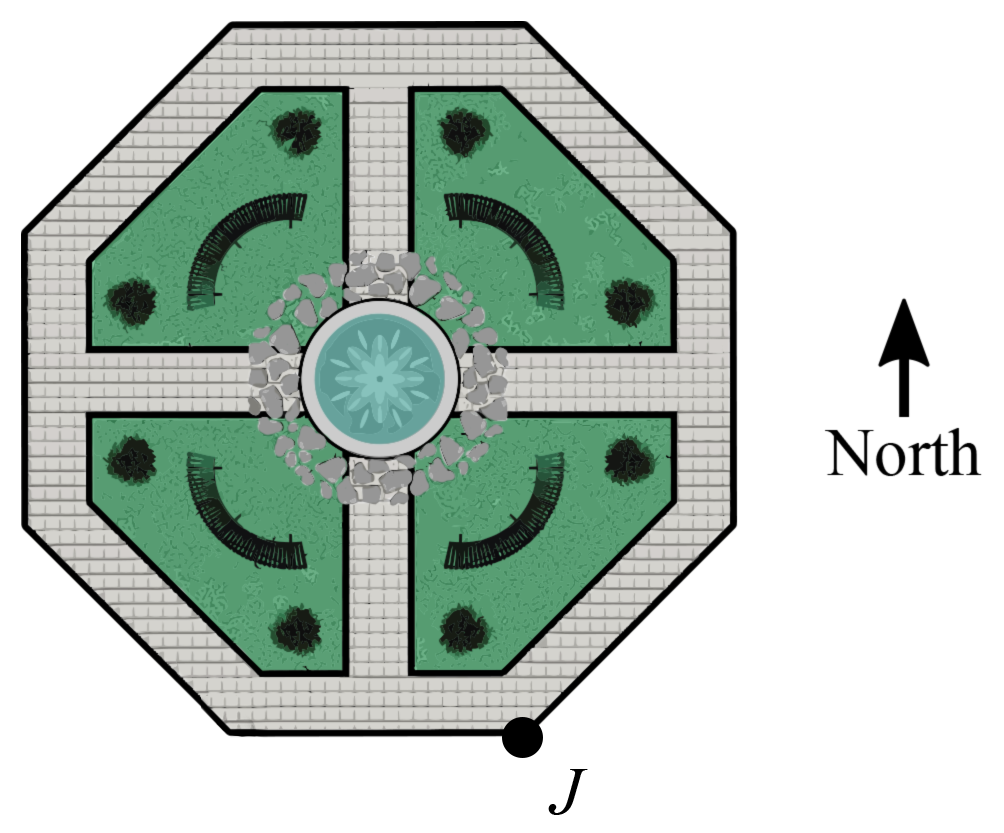
Shivansh walks around a section of the gardens at The Taj Mahal.

He starts at point JJ and walks west.

If he walks 35\dfrac{3}{5} of the distance around the garden, in what direction is he heading?


Worked Solution

Each edge = 18\dfrac{1}{8} of a full circuit.

Since  12\dfrac{1}{2} < 35\dfrac{3}{5} < 58\dfrac{5}{8}

∴\therefore Shivansh is heading east.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Shivansh walks around a section of the gardens at The Taj Mahal. He starts at point $J$ and walks west. If he walks $\dfrac{3}{5}$ of the distance around the garden, in what direction is he heading?
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-q-var2.png 320 indent3 vpad
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-sol-var2.png 360 indent vpad Each edge = $\dfrac{1}{8}$ of a full circuit. Since  $\dfrac{1}{2}$ < $\dfrac{3}{5}$ < $\dfrac{5}{8}$ $\therefore$ Shivansh is heading east.
correctAnswer
east

Answers

Is Correct?Answer
x

west

✓

east

x

south

x

north

Variant 3

DifficultyLevel

642

Question

Clifford walks his dog around his local park.

He starts at point JJ and walks south.

If he walks 25\dfrac{2}{5} of the distance around the park, in what direction is he heading?


Worked Solution

Each edge = 18\dfrac{1}{8} of a full circuit.

Since  38\dfrac{3}{8} < 25\dfrac{2}{5} < 12\dfrac{1}{2}

∴\therefore Clifford is heading north-west.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Clifford walks his dog around his local park. He starts at point $J$ and walks south. If he walks $\dfrac{2}{5}$ of the distance around the park, in what direction is he heading?
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-q-var3.png 320 indent3 vpad
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-sol-var3.png 360 indent vpad Each edge = $\dfrac{1}{8}$ of a full circuit. Since  $\dfrac{3}{8}$ < $\dfrac{2}{5}$ < $\dfrac{1}{2}$ $\therefore$ Clifford is heading north-west.
correctAnswer
north-west

Answers

Is Correct?Answer
x

north

x

south

✓

north-west

x

south-west

Variant 4

DifficultyLevel

628

Question

Jackson walks around his local park.

He starts at point JJ and walks south-east.

If he walks 15\dfrac{1}{5} of the distance around the park, in what direction is he heading?


Worked Solution

Each edge = 18\dfrac{1}{8} of a full circuit.

Since  18\dfrac{1}{8} < 15\dfrac{1}{5} < 14\dfrac{1}{4}

∴\therefore Jackson is heading west.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Jackson walks around his local park. He starts at point $J$ and walks south-east. If he walks $\dfrac{1}{5}$ of the distance around the park, in what direction is he heading?
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-q-var4.png 330 indent3 vpad
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-sol-var4.png 360 indent vpad Each edge = $\dfrac{1}{8}$ of a full circuit. Since  $\dfrac{1}{8}$ < $\dfrac{1}{5}$ < $\dfrac{1}{4}$ $\therefore$ Jackson is heading west.
correctAnswer
west

Answers

Is Correct?Answer
x

east

x

north

✓

west

x

south

Variant 5

DifficultyLevel

641

Question

Yui walks around the centre garden at the amusement park.

She starts at point JJ and walks west.

If she walks 45\dfrac{4}{5} of the distance around the garden, in what direction is she heading?


Worked Solution

Each edge = 18\dfrac{1}{8} of a full circuit.

Since  34\dfrac{3}{4} < 45\dfrac{4}{5} < 78\dfrac{7}{8}

∴\therefore Yui is heading south.

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Yui walks around the centre garden at the amusement park. She starts at point $J$ and walks west. If she walks $\dfrac{4}{5}$ of the distance around the garden, in what direction is she heading?
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-q-var5.png 330 indent3 vpad
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/07/NAPX-E4-CA22-sol-var5.png 365 indent vpad Each edge = $\dfrac{1}{8}$ of a full circuit. Since  $\dfrac{3}{4}$ < $\dfrac{4}{5}$ < $\dfrac{7}{8}$ $\therefore$ Yui is heading south.
correctAnswer
south

Answers

Is Correct?Answer
x

north

x

east

x

west

✓

south

Tags