Number, NAPX-p167381v01

Question

The image below is the plan of a farming plot.

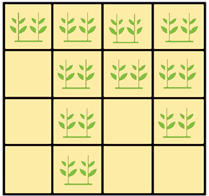
Squares containing plants represent land that is growing crops.

Which fraction shows the amount of land that is used for growing crops?

Worked Solution
Fraction = Squares growing cropsTotal squares\dfrac{\text{Squares growing crops}}{\text{Total squares}}
= 1016\dfrac{10}{16}
= {{{correctAnswer}}}

Variant 0

DifficultyLevel

446

Question

The image below is the plan of a farming plot.

Squares containing plants represent land that is growing crops.

Which fraction shows the amount of land that is used for growing crops?

Worked Solution
Fraction = Squares growing cropsTotal squares\dfrac{\text{Squares growing crops}}{\text{Total squares}}
= 1016\dfrac{10}{16}
= 58\dfrac{5}{8}

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
correctAnswer
$\dfrac{5}{8}$

Answers

Is Correct?Answer
x

45\dfrac{4}{5}

✓

58\dfrac{5}{8}

x

12\dfrac{1}{2}

x

38\dfrac{3}{8}

Tags