Number, NAPX-J3-CA09

Question

{{{question}}}

Worked Solution

{{{workedSolution}}}

Variant 0

DifficultyLevel

501

Question

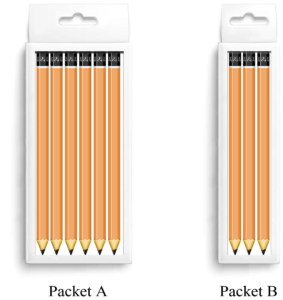
Pamela is a teacher and buys pencils for her class.

She purchases the pencils in two different sized packets.



Pamela buys 6 packet A's and 4 packet B's.

She then divides all the pencils equally among her 6 students.

How many pencils does each student receive?

Worked Solution
Total pencils = (6 × 6) + (4 × 3)
= 48
∴\therefore Pencils per student = 48 ÷ 6
= 8

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Pamela is a teacher and buys pencils for her class. She purchases the pencils in two different sized packets.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2017/09/NAP-J1-CA09-283x300.png 300 indent3 vpad
Pamela buys 6 packet A's and 4 packet B's. She then divides all the pencils equally among her 6 students. How many pencils does each student receive?
workedSolution
||| |-|-| |Total pencils| = (6 × 6) + (4 × 3)| || = 48|
||| |-|-| |$\therefore$ Pencils per student| = 48 ÷ 6| || = {{{correctAnswer}}}|
correctAnswer
8

Answers

Is Correct?Answer
x

6

x

7

✓

8

x

42

x

48

Variant 1

DifficultyLevel

501

Question

John bought bread rolls that came in bags of 4 and bags of 6.



He bought 5 Bags A's and 10 Bag B's.

John then divided the bread rolls equally among 20 families.

How many bread rolls did each family receive?

Worked Solution
Total bread rolls = (4 × 5) + (6 × 10)
= 20 + 60
= 80

∴\therefore Bread rolls per family = 8020\dfrac{80}{20}
= 4

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
John bought bread rolls that came in bags of 4 and bags of 6.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2021/04/RAPH10-q45.svg 350 indent3 vpad
He bought 5 Bags A's and 10 Bag B's. John then divided the bread rolls equally among 20 families. How many bread rolls did each family receive?
workedSolution
||| |-|-| |Total bread rolls|= (4 × 5) + (6 × 10)| ||= 20 + 60| ||= 80|

||| |-|-| |$\therefore$ Bread rolls per family|= $\dfrac{80}{20}$| ||= {{{correctAnswer}}}|
correctAnswer
4

Answers

Is Correct?Answer
✓

4

x

5

x

6

x

70

x

80

Tags