20317

Question

{{{question}}}

Worked Solution

{{{workedSolution}}}

Variant 0

DifficultyLevel

623

Question


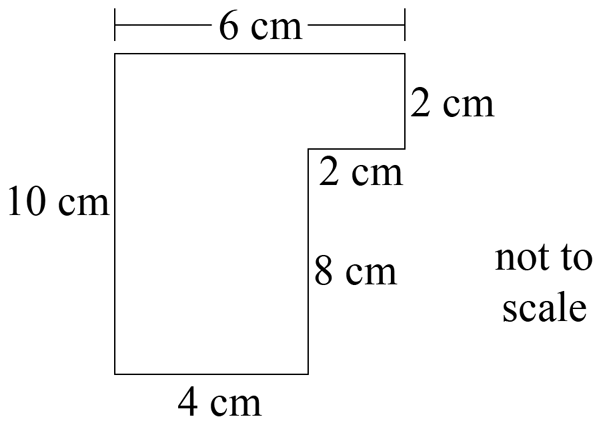
Which of these could be used to calculate the area of the shape in square centimetres?

Worked Solution
Area = Area of large rectangle −- Area of cut-out rectangle
= (10 ×\times 6) −- (8 ×\times 2)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2017/01/NAP-H3-CA23.png 240 indent vpad

Which of these could be used to calculate the area of the shape in square centimetres?
workedSolution
| | | | --------------------- | -------------------------------------------- | | Area | = Area of large rectangle $-$ Area of cut-out rectangle | | | = {{{correctAnswer}}} |
correctAnswer
(10 $\times$ 6) $-$ (8 $\times$ 2)

Answers

Is Correct?Answer
x

(10 ×\times 4) + (6 ×\times 2)

x

(10 ×\times 6) − (8 ×\times 4)

x

(10 ×\times 8) + (2 ×\times 4)

✓

(10 ×\times 6) −- (8 ×\times 2)

Variant 1

DifficultyLevel

623

Question

Which of these could be used to calculate the area of the shape in square centimetres?

Worked Solution
Area = Area of large rectangle −- Area of cut-out rectangle
= (13 ×\times 18) − (3 ×\times 13)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_20317_v1.svg 350 indent vpad
Which of these could be used to calculate the area of the shape in square centimetres?
workedSolution
| | | | --------------------- | -------------------------------------------- | | Area | = Area of large rectangle $-$ Area of cut-out rectangle | | | = {{{correctAnswer}}} |
correctAnswer
(13 $\times$ 18) − (3 $\times$ 13)

Answers

Is Correct?Answer
x

(10 ×\times 18) + (13 ×\times 5)

x

(13 ×\times 18) + (10 ×\times 3)

x

(10 ×\times 18) −- (5 ×\times 3)

✓

(13 ×\times 18) − (3 ×\times 13)

Variant 2

DifficultyLevel

623

Question

Which of these could be used to calculate the area of the shape in square millimetres?

Worked Solution
Area = Area of large rectangle −- Area of cut-out rectangle
= (21 ×\times 18) − (17 ×\times 15)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_20317_v2.svg 300 indent vpad
Which of these could be used to calculate the area of the shape in square millimetres?
workedSolution
| | | | --------------------- | -------------------------------------------- | | Area | = Area of large rectangle $-$ Area of cut-out rectangle | | | = {{{correctAnswer}}} |
correctAnswer
(21 $\times$ 18) − (17 $\times$ 15)

Answers

Is Correct?Answer
✓

(21 ×\times 18) − (17 ×\times 15)

x

(4 ×\times 18) −- (21 ×\times 3)

x

(21 ×\times 4) + (18 ×\times 17)

x

(4 ×\times 18) + (21 ×\times 3)

Variant 3

DifficultyLevel

624

Question

Which of these could be used to calculate the area of the shape in square centimetres?

Worked Solution
Area = Area of large rectangle −- Area of cut-out square
= (16 ×\times 11) −- (9 ×\times 9)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_20317_v3.svg 390 indent vpad
Which of these could be used to calculate the area of the shape in square centimetres?
workedSolution
| | | | --------------------- | -------------------------------------------- | | Area | = Area of large rectangle $-$ Area of cut-out square | | | = {{{correctAnswer}}} |
correctAnswer
(16 $\times$ 11) $-$ (9 $\times$ 9)

Answers

Is Correct?Answer
x

(3 ×\times 11) + (14 ×\times 11)

✓

(16 ×\times 11) −- (9 ×\times 9)

x

(11 ×\times 16) −- (9 ×\times 5)

x

(11 ×\times 8) + (16 ×\times 2)

Variant 4

DifficultyLevel

624

Question

Which of these could be used to calculate the area of the shape in square centimetres?

Worked Solution
Area = Area of large rectangle −- Area of cut-out smaller rectangle
= (17 ×\times 20) −- (16 ×\times 7)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_20317_v5.svg 400 indent vpad
Which of these could be used to calculate the area of the shape in square centimetres?
workedSolution
| | | | --------------------- | -------------------------------------------- | | Area | = Area of large rectangle $-$ Area of cut-out smaller rectangle | | | = {{{correctAnswer}}} |
correctAnswer
(17 $\times$ 20) $-$ (16 $\times$ 7)

Answers

Is Correct?Answer
x

(20 ×\times 17) + (7 ×\times 3)

✓

(17 ×\times 20) −- (16 ×\times 7)

x

(20 ×\times 10) −- (7 ×\times 16)

x

(7 ×\times 20) + (20 ×\times 3)

Variant 5

DifficultyLevel

602

Question

Which of these could be used to calculate the area of the shape in square centimetres?

Worked Solution
Area = Area of large horizontal rectangle + Area of small vertical rectangle
= (9 ×\times 3) + (5 ×\times 2)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_20317_v4.svg 350 indent vpad
Which of these could be used to calculate the area of the shape in square centimetres?
workedSolution
| | | | --------------------- | -------------------------------------------- | | Area | = Area of large horizontal rectangle + Area of small vertical rectangle | | | = {{{correctAnswer}}} |
correctAnswer
(9 $\times$ 3) + (5 $\times$ 2)

Answers

Is Correct?Answer
x

(9 ×\times 8) −- (3 ×\times 5)

✓

(9 ×\times 3) + (5 ×\times 2)

x

(8 ×\times 9) −- (4 ×\times 5)

x

(3 ×\times 9) −- (2 ×\times 8)

Tags