30062

Question

Mark and Jim have property sizes as shown in the table below:



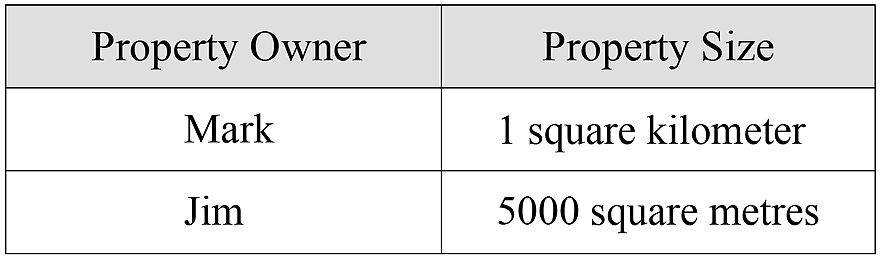
What is the ratio of the land area of Mark's property to Jim's property.

Worked Solution

1 km2=1000 m×1000 m=1 000 000 m2\begin{aligned} 1\ \text{km}^2 &=1000\ \text{m} \times 1000\ \text{m} \cr &=1\ 000\ 000\ \text{m}^2 \end{aligned}

Ratio=1 000 000:5000=1000:5=200:1\begin{aligned} \text{Ratio} &=1\ 000\ 000 : 5000 \cr &= 1000 : 5 \cr &=200 : 1 \end{aligned}

Variant 0

DifficultyLevel

685

Question

Mark and Jim have property sizes as shown in the table below:



What is the ratio of the land area of Mark's property to Jim's property.

Worked Solution

1 km2=1000 m×1000 m=1 000 000 m2\begin{aligned} 1\ \text{km}^2 &=1000\ \text{m} \times 1000\ \text{m} \cr &=1\ 000\ 000\ \text{m}^2 \end{aligned}

Ratio=1 000 000:5000=1000:5=200:1\begin{aligned} \text{Ratio} &=1\ 000\ 000 : 5000 \cr &= 1000 : 5 \cr &=200 : 1 \end{aligned}

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
correctAnswer
200\:1

Answers

Is Correct?Answer
x

2:1

x

5:2

✓

200:1

x

250:1

Tags

  • ms_ca