20294

Question

A resort has 4 pools.

Which pool has the largest surface area?

Worked Solution

Consider the surface area of each pool:

1st pool = 6 ×\times 19 = 114 m2^2

2nd pool = 7 ×\times 18 = 126 m2^2

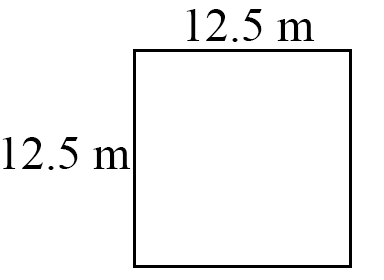
3rd pool = 12.5 ×\times 12.5 = 156.25 m2^2

4th pool = 10 ×\times 15 = 150 m2^2

∴\therefore The 3rd pool, 12.5 × 12.5, has the largest surface area.


{{{correctAnswer}}}

Variant 0

DifficultyLevel

528

Question

A resort has 4 pools.

Which pool has the largest surface area?

Worked Solution

Consider the surface area of each pool:

1st pool = 6 ×\times 19 = 114 m2^2

2nd pool = 7 ×\times 18 = 126 m2^2

3rd pool = 12.5 ×\times 12.5 = 156.25 m2^2

4th pool = 10 ×\times 15 = 150 m2^2

∴\therefore The 3rd pool, 12.5 × 12.5, has the largest surface area.


Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
correctAnswer
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2017/02/naplan-Y7-2009-9mciii.png 150 indent vpad

Answers

Is Correct?Answer
x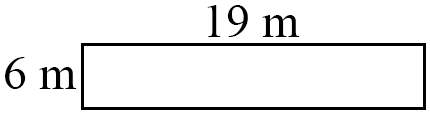
x
✓
x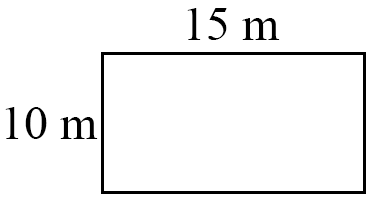

Tags

  • ms_ca