50043

Question

{{{question}}}

Worked Solution

{{{workedSolution}}}

Variant 0

DifficultyLevel

620

Question

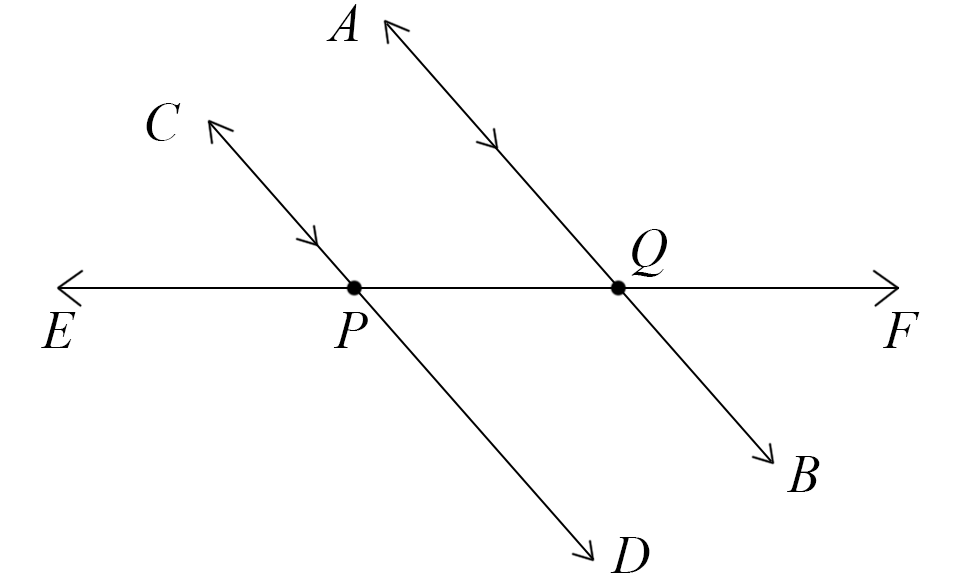
Lines ABAB and CDCD are parallel.

Line EFEF intersects lines ABAB and CDCD as shown.



Which pair of angles are equal?

Worked Solution

∠\angleCPQ and ∠\anglePQB

(Alternate angles)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Lines $AB$ and $CD$ are parallel. Line $EF$ intersects lines $AB$ and $CD$ as shown.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2016/12/naplan-2016-20mc.png 320 indent vpad
Which pair of angles are equal?
workedSolution
{{{correctAnswer}}} (Alternate angles)
correctAnswer
$\angle$CPQ and $\angle$PQB

Answers

Is Correct?Answer
x

∠\angleFQA and ∠\angleFQB

x

∠\angleCPQ and ∠\angleAQE

x

∠\angleDPE and ∠\angleDPF

✓

∠\angleCPQ and ∠\anglePQB

Variant 1

DifficultyLevel

621

Question

Lines ABAB and CDCD are parallel.

Line EFEF intersects lines ABAB and CDCD as shown.



Which pair of angles are equal?

Worked Solution

∠\angleFQA and ∠\angleQPC

(Corresponding angles)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Lines $AB$ and $CD$ are parallel. Line $EF$ intersects lines $AB$ and $CD$ as shown.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2016/12/naplan-2016-20mc.png 320 indent vpad
Which pair of angles are equal?
workedSolution
{{{correctAnswer}}} (Corresponding angles)
correctAnswer
$\angle$FQA and $\angle$QPC

Answers

Is Correct?Answer
✓

∠\angleFQA and ∠\angleQPC

x

∠\angleCPQ and ∠\angleAQE

x

∠\angleDPE and ∠\angleDPF

x

∠\angleCPQ and ∠\angleFQB

Variant 2

DifficultyLevel

622

Question

Lines ABAB and CDCD are parallel.

Line EFEF intersects lines ABAB and CDCD as shown.



Which pair of angles are equal?

Worked Solution

∠\angleAQP and ∠\angleQPD

(Alternate angles)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Lines $AB$ and $CD$ are parallel. Line $EF$ intersects lines $AB$ and $CD$ as shown.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2016/12/naplan-2016-20mc.png 320 indent vpad
Which pair of angles are equal?
workedSolution
{{{correctAnswer}}} (Alternate angles)
correctAnswer
$\angle$AQP and $\angle$QPD

Answers

Is Correct?Answer
x

∠\angleCPQ and ∠\angleAQE

✓

∠\angleAQP and ∠\angleQPD

x

∠\angleDPE and ∠\angleDPF

x

∠\angleCPQ and ∠\angleFQB

Variant 3

DifficultyLevel

623

Question

Lines ABAB and CDCD are parallel.

Line EFEF intersects lines ABAB and CDCD as shown.



Which pair of angles are equal?

Worked Solution

∠\angleFQB and ∠\angleQPD

(Corresponding angles)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Lines $AB$ and $CD$ are parallel. Line $EF$ intersects lines $AB$ and $CD$ as shown.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2016/12/naplan-2016-20mc.png 320 indent vpad
Which pair of angles are equal?
workedSolution
{{{correctAnswer}}} (Corresponding angles)
correctAnswer
$\angle$FQB and $\angle$QPD

Answers

Is Correct?Answer
✓

∠\angleFQB and ∠\angleQPD

x

∠\angleAQF and ∠\angleQPD

x

∠\angleCPQ and ∠\angleAQE

x

∠\angleDPE and ∠\angleDPF

Variant 4

DifficultyLevel

624

Question

Lines ABAB and CDCD are parallel.

Line EFEF intersects lines ABAB and CDCD as shown.



Which pair of angles are equal?

Worked Solution

∠\angleCPE and ∠\angleAQP

(Corresponding angles)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Lines $AB$ and $CD$ are parallel. Line $EF$ intersects lines $AB$ and $CD$ as shown.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2016/12/naplan-2016-20mc.png 320 indent vpad
Which pair of angles are equal?
workedSolution
{{{correctAnswer}}} (Corresponding angles)
correctAnswer
$\angle$CPE and $\angle$AQP

Answers

Is Correct?Answer
x

∠\angleAQF and ∠\angleQPD

x

∠\angleCPQ and ∠\angleAQE

✓

∠\angleCPE and ∠\angleAQP

x

∠\angleDPE and ∠\angleDPF

Variant 5

DifficultyLevel

645

Question

Lines ABAB and CDCD are parallel.

Line EFEF intersects lines ABAB and CDCD as shown.



Which pair of angles are supplementary?

Worked Solution

Supplementary angles sum to 180°\degree

∠\angleCPQ and ∠\angleAQP

(Cointerior angles are supplementary)

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
Lines $AB$ and $CD$ are parallel. Line $EF$ intersects lines $AB$ and $CD$ as shown.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2016/12/naplan-2016-20mc.png 320 indent vpad
Which pair of angles are supplementary?
workedSolution
Supplementary angles sum to 180$\degree$ {{{correctAnswer}}} (Cointerior angles are supplementary)
correctAnswer
$\angle$CPQ and $\angle$AQP

Answers

Is Correct?Answer
x

∠\angleAQF and ∠\angleCPQ

✓

∠\angleCPQ and ∠\angleAQP

x

∠\angleCPE and ∠\angleAQP

x

∠\angleDPE and ∠\angleBQP

Tags