Number, NAPX-p73124v02
Question
{{{question}}}
Worked Solution
{{{workedSolution}}}
U2FsdGVkX18hVlqYIiq/HBaBNNH1RIvHrcZEdO1oXpqRi/WYmkXo3Zz57YdEX6TffhdjHmXK/VA/oVGrS4fu91iHmTe/Y3HGFi8EsJQQwUYHsRH7+m2EDllZhGJ7uKfrSDNf7VjegWRo2S1nPQqCyYlzuuIjkT+r+e/bQG9BWqHfkUTUPOVgdLiOK3LhGdV2MEtcXQMJV2Bi1xoXBzmSm8jFpyWvm+IQ4J1c9wCPt+g8bfaspx9L/QqwqMlWMBuKd3XTaeZOm/KEPA5ucnHd4RYU7SrRGYtiwjQuVtd5MHuLIptBeOZ6cE2saGKISP5JCb7mSBxwGNQ9uh1rj2JKOXtM0eUF+go7zrN8kSyoGoOIg6fNqRetjEbp2Bt+/XdQhurfm3I8TeabMNbWfKh60O+VtR6fBFnAMA5lq6A6oSJPQFD5VFs2QziYphERfjJGn0MFX2imrlNpa5RtcMP8lpwv5mkVYunVve6HuO9pLfEq34SHW7VeazuBkUckHU/ksbhYgIEj0JTENbbhi+6g5WF7QSAK0Nm/rFOZllOtwBMp0bBHgqkB3HDtqkuedCwpUTbVftp6vXUljk+537w79GGvpbgchbvitJWW3pM16aJs/STdwThejAl0vVtSSw3nwCj6IN1P3uNDoYEqe8zafcWxHvKCDihwdsN/sJ3qynGN2QL86I6mCUak2sXCuhQZly9qELQZgfnpQRhm9dFi1AnZ20tFhOl0FzK5dvcrvooM6pZ4QYZjUDFNSf/LpVVGs41TMNyLXfgSf9DHbnhr8O46JJy1l6usPassQ0Sr8Qkq6o+yyRt9H5JMesohbnSI4twksHd/UH4y1rKtt8osuxq5SJics3eRgdlAcQj2rTI3by3ERjtzFeZmhBJ/4EJVZsXZ2Gv0WckMFVbdoPruiZ3LNs4hynl8Mfl58Glet6T9B1DY5CHP0q4UwQ92UlHjtLsCc7Y/Mdq+YHzLRUdDrEvzjVmbajxuVvDTNCsYiLL5QClL4XzKGpVV2IwERnNK6HHFVi5oFh8ggyop/vy+EcIapkJsJe1b0Ds2/jifqswz3vPM2OoZAtQNFFob+/pHQDAJtGCV/9qXceMeab4+4lrT6FwcBDeQZS2zuabP4/bw2MPDJpx6ciTUQ+NhGRk9dI+SJUpQ88m6I5L6pa1w+E+iOzJX0YoBqZUgMWjXGxUpUSgOGAOf+A9hfHZ6W4RyUzjxCJ9Qi1UOpUmino1HLrLNGUW+YmlxFQAR9znQdIUK1XK0pWiav13UScOEMk+tcl89f3mmu4J5d/4ZWFspDieufyRDy0nPLxZCagbwx+UQgFDxZ/Y82tOuD4zPE+IiYxRrtflCbpk3KbPkd3DcirPGmHweRh9youarbr1MpDNFTg2Iawtaw4v8/N7OCEgze0VTLMPqDVbEVF6rizT2TmyFCUyLqAEw94cA7nAfx//XoBpo5i1bwRN/PFPbIZAbxRDRhycZ0wq89XvsK3wEFFlZZvcYrd3wnXRTM3CLJorIv7CbNRLzcjWbLQnrBCZD7Ei2McI9k2ff1BOqT2Yg+gFld7y2vZePqVGH4tqWbR5/K9A7r503CsV99LMJC0b00o8o6fIdawpjp/j3yYTT6KyE9uYcIAY4Piy+J8wIJs78KBWZBEd5ntOLdvyHqOw2B1PDLuRHvm60XvbFkeT+ixMkSGX321BYxzu4zsoaljrrHfe46JX0DsSuun4hpxr5NKVUIqg/jceXWy3f3V1qWbnaoB32A3oqVsnoNe1UqR2NN212ilCrnYAhDxoijil5UHYywgTMbAsbd4fk3PTBl61QSuUgeuyGkrc+3nVzB3BZse1VWyuFuBiFHc2UqlhdOa1mchCf4E5eeQC/gF0T0OJ1FZ5Wj+ZYzZIYMz301QHHGmwhH3RZTd3JVcCHLSFWYXMZM/lMg8Q+jcdK8NZw6EEqu3697Qe/ccO3/nSdjPXAk3U10GvnSW/H5jEr7bjWIjl4ezqP/Jb7V9H5wsRUe0s9imLJ9GGvUQ/vmtSWfA4pMn9n9WwgCvKAts242vzgt2GpBiULxm3WNHZ5pFRHsyAZmO3zX0W9u9vXw0TfsP9+BVwwAYcZp9to1hgcYVLA3fAzy3dEZOg6UjxJ3cUQaKhq33EUwR92Bxf+MPmxhF3QnWolDU7NPUTApUfM+mi/6lZ0c+tFFrKEGH3gF6aoPfBIquW+eXC0RB+GCbdCCJd2J7r662mMr2Z3LJxtcNA0BBQ4wYe4yjhUj43lZysFuEN8V9Omp50AERXtXLYEg8mCHBxsRadMk5E/QsUTYrxQcZY1HYI7xUvoJoL5BXzuq4Y2XZSZZt/iFWE5bzYMi6NT/fUrUynGOivSpG0nKIQx/sDcT76v8EYKNB5XZzrdP6lKMyS3n33iKNn6MoEoUKS+pHUj/YlzU0dcRIhXLpzzLRxVAJy9+JyG6+ktqp/jwkjvNxGUertZ5yRDwja7zYwy6HnCz2DHUfAPdMn/MNwh19IBxBcMQby3/7s13CGTNzXsc9V8HQcBipiE5x5456SfS0jGhnaHWzd5MwlwOmUXrfAvy+JjaYxPs9jSjxzsfZ63EqI9XUYrF8WDT3Dqo2S+FcbK0xEAM+IJTVbPnNk5pFgtWW2JYEhNtg5eesVtJqOaVp1KAA9zW/1Wm91469UdPXgEAi/r7dsMB+dQ0QKbyVRXegDiFk3IkavbJ+u81z87krAN93EvVrr7QpD8FOp5zRp5f9XHuTGzIQzFIs8XROxU0dEOCQda2t4v/+HwmBB7/XEcAvBwniUSyHkfa5eonoXvDhZvf0Vcz/pvSCntDnA938Wt+iT3CA9LFs3DHB5mOH77CPUwKeN8AuKUebzXUbpncgGIzbLbWXe93iY9MExO9NRsoznjmNL5PW5zdtU8m0ERDBTdKclSdVcDHTOiV7qdDVZdrUwqiJF6qrnReQSWNFesGXCJMuRK6BZFU6cyR8drAf/XWtvFGznpx6w1kC1NUB/8rz49Cku6ZH74LIOdXT7/pizySir+hmMrLaI5Fe7S/r4HZE7qnQsP4wPAGTWtJx5ILs2WL6TRhqOIleN4kTvvQzvoZAe7cnJRa3F0DclZ0T2aAWE3wvI7SZIFbmeZeSyButo7b1M54tjxiyEXKRs2AmWeMySrDlo1ta6gFkVwUul3/QyRiHlVlzMPtIf/RiQxrABhYteAgHebj47mbWbtWy+hKlFck1tFwb6ViGd+o522fbSo004BATH8K/QCi/LGIDIqRZoYeAdZ3UbEn4rqtyh6388yLZRKOF7XL/TN281WoPaUjRZkyPcCKd2qxAESYojDgxrx7K14rR4WzGxVGQ5Dk9y2BU1FtsW8S/hHCDxemWpkkYzBRisfXLPHxf7NW4s3lJqfVdrsE3JGcD+4yLGyoEIAAaPX6mSrWeqqkw/IpgXxDJaK/aeszuOghZgKoVop2xEn+tmfAcej2tfYvA+zXGpcbzE7L+STtTc4unTLupPe096RamsDliBX6/lF0WobA3Xi5wXD0BcXDTsMO0fDx8OEdtWONHmrrr1c0I75O3M/iSJkelydKR8ytnBw/T9F5f1zxfSI/yvQ62FGpcN1hWZtgcVJepuUbHhJ2F9PMZEyrG9qzAUwU4qYOb/1Q1CUC+UINQ+yq5yJgbXrJFDr8dC0gfObcIlbztTcwzZBFz0R8taVrD6qMn2tldvuLvk2mNvZ4hgpIIdeNfZmDzNyMTd7lH1fuH4EcN88C/iCTDg4n3aB6blDDbQvsCU5FKUf3A0KbyFz5qL2HYyvWPSzy7xbw/kHbr4HEKNoDGt/33QpZp5tD3d9sFguFojn8OlrnTOfEP0gBNm9evKBF/+WieAeWaD+y/TJnBC3GpOr/3w7Oz33gfRJIadgtH3Vdxkc8yAFP+vQHN0IWLcy8OMO3iLq6Q14zOP2lsldgX/oKs/XTZPFUj+FZFLWWysrKLiVlt9DnAsWADHylfn/saj3kPHWL5TthSejM3LbYqQ+4v9nJNM/t2HRTlUAUY0z3211+08d9qjWYeRmWh9HKY7af+0lIdAsUQKYpw0YVlpae5Czlz8fV7Cpy5RaK/bX8b74RkecJ2QDnZ93BfKbrWgkY9eSCMoocmAATK4E43LlL2KGnaEVyLyzJ90K0DmL/Zu3wljZ4vClzw1h98HAeuLOTDnhaKieQmWDWoByduXJTFcXuUz6BfVAIhQ7kqJXgMSJQqaVh+t01bCzEDKGPMapJdcWf/SxjqfUqFg4aBzj1RfTtyNOcE+0uWdkiFlJ3P3jYLDrMEaDKIEDjNhtMtzNWvGr9accjZmX1H5BRhhofxfgXqQH7fynhEf/uE5ImSrWGof/VRsWUN93/+qWQV4iKcYppINtWsJhLE1/aXt06Ltto4AOOOrfkgtoLB7WIP8jPinTsggPmZ3cHEn+pQ9WG89mv4C+3w84za3hh1M45MhK/+CPIHDyj8T/vGeJXq1yG3hYt8j+k8YyIoot+Mmg5YP3uiXuKoy93RO76Ip93F7zJ4PRqKP0hBHjzV8nfdz9lmxEF0tLP6x14J7cxjuXyAWSaGho5c4fDFH32Qm2bOICuEWRGBZ1rAJGPlQmdJ2v2CUn5FWKbYPgPRCsDswzuXxNhkO28hb941AIwfQgnMxt23UPs0KZVWYn0042ORy94dqPrWSnM3QheAk1FGNcYWi6t4S3J4tGR8KIfJP3CVgytyGxgJVyicnfZjZKK6baBnRlBvDioYHOyYCHxmfT2rZntmerE7kLaW20fQv3TGfu2PudOowc9tJJMhEh0qFaMSjM2BPJjr2gnK+J0aI8y07xc47U9qTMVJBJi4CWwxt0XvXo7aFHBjq+w4uW6SOC3yAAY+4hPfdDD6ACq9AJlvTD52JSFGPeFSjDyLODoqxI73khdZerqR6bT6iSK1CKVqhQBDebfh0JiOPmoP48/pSsRn7jTahDKTExJ5XZiVElfx8GZGuNh2Z9EfrPnZSwNIqDxiw+oF7ilbaw8saH60wpUxSh3Fy0kOfuj68XOv4k6j9T7j9OKYj5vj5v/AMue7Ex3jxX+DB4U8pC912wp4TwtuiJDwCqRHTukMAKRwDpu/GVRJhgtMsoTTAxHek+0vzz3mUk6HTKKV42mJ09C9E6okUoP0mf4/XPBquXiOQ6a46Y0fb79Eh0Vae/6dTz5Ojmzt6K1ck0ElgqKrYNtsz+E8qR2MRk0vQF2t3nfTy4sT1RQownfgEhiQw6eSRpFbvfBV5XKXAtUcgvE/ySOaAJ0v6HErwhdy9MZp9fkyy7XsNWZnATS+nkf2mEB6NDqmpFbHK1OihYHFkkBOE9WCAI9hrJ2niugFAVqxxGq06uk2aKowRvuy/+mQVZnyJ8O2JPfeeuP3MQu5szTk1i7/npkmYB3iDQZbzs3tdsMEWkRY20ud6KxmFot98c93AXiwzP8EczBtd8lQLiNzjH7HMk4dSOYEhlBXmIdH8ljTPFTvA/n9GJoDPU2i+t1S/di1g7U7qzh24mUA6y94DP687W7JUPqhDvdGvl04wK9JHx828UJsTcC3xWJwyQPCMq9iPLAxowbH4kzWDmvuOoDxHdYi0rie+0Iokw88i0BmAuuOK47V8/mu/t5ZGdxMfdNOQOcwMNZ2QHyNWMvxO5aLxQxbiDMIaqUrISaa2zvA0kvaFiJ6bROcyjMw0w/JMPlCnfLZTnifv7PXJefDVtDZFJeLsdNJCR+a/VD2MBfnqv/EWtnm1nEsUERK+khTUNMZbPzsxFQna+hT6YY5j2HPpylZOyfo1ZsDp4b4VKg/mAIzXrs8DmfENCBGrf5I/tbyySETOqHjMAD8HrcQJk7fFZ/xjxoL/BS8BWRsh3zXMMWn/TKA57FpWyFRo+1w+lhzaOHDa2A/byEcnRCHR2xWUpKZIeXA==
Variant 0
DifficultyLevel
530
Question
Julian was driving into town and hit a kangaroo 43 of a kilometre into his trip.
Which of these represent where Julian hit the kangaroo?
Worked Solution
Each spacing is worth 41 km.

Question Type
Multiple Choice (One Answer)
Variables
| Variable name | Variable value |
| question | Julian was driving into town and hit a kangaroo $\dfrac{3}{4}$ of a kilometre into his trip.
Which of these represent where Julian hit the kangaroo? |
| workedSolution | Each spacing is worth $\dfrac{1}{4}$ km.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2021/04/Number-NAPX-p73124v02-iv.png 240 indent vpad |
| correctAnswer | sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2021/04/Number-NAPX-p73124v02-iv.png 240 indent vpad
|
Answers
| Is Correct? | Answer |
| x |  |
| x |  |
| x | 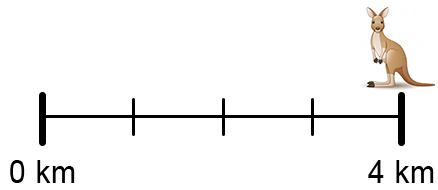 |
| ✓ |  |
U2FsdGVkX18oPFytObX4CB5bhdrGNy9fkTgyaTjk4CAgXd5FLC+z0LVRJDhi2HHK1isQcVH+iNwMPz5ooFES41bEeI3Ng37ofWfs6AgQLlELA0R8fmZkxktKRCEPmQanXp+SQ3Y1u0MkJaQypmGOPQ6H6E9KGe9nE23aws3sUg81OKGTK5rMgFoZ+NW6davEXm0SchefRTJa3OkGiZrPQIiXZAA/fYTrxbf8tVcclr3X6PWZU9GnYJpdyno4fHfKV6lRKG/CZb+T4mRzwCoiKGEyHoNmoXpSLPbrgdUxyIF1MCKAcb5dO5S4WPAr6b+5QnDik1lBC/6qvrErIKqcEb3P2veKdywCtVttxbmXXbl6E72gRrUSyQ/GfUxeo/sYIvd2R7wmH+P0Dbj9gg5Jl/doOddKbefG+78rErYsL5NJx2MRE3Nw6JOyI4P7ZGE3wYAyn77EmtlVaQjdd8TeIq3OJd5FXQBp4sNNQLCvQaqW1SKoMITc0f/3Ng+yabkXjJvvBA45a6oMXQ5zqqpFcdguZOm0TPV0nkwzkoztHyux8qvzaobHkbpC0XQyT0cmlTsBQvkC+e26zbV80Iz51k7kO0E6GAuJTaFbtz3IyBhKVOZvX9YfdVYkDnWhtJMaMJQMqjP8WcRYVjT5bIOJa105qoAH6VbCCj3rt6qpe/HdA37cLZ3SbQaRMcGF9H9bkrMSTUobdq6vkVqLi2LBbLN2z+jYouXaNekC0NyjJa0aikihpDN82EjEREekiFrYhpiVqXEXHDHPy+CHozh60b7+H5t10LQvoJaIrXOX5S9acUN3Oz1XEbwN9vNwcy7UqzM9GzAIPhaopyS9knTZI9Pm7lifwvF58WqQiR30HskPKtqivTKhw9zwNPSSju5p45CmeJNyEG7LnF++1nPxy4rAoPqnte4lVtT0qBFKZRBvkdYTIYMpzHmzLNHGMTrdrGgzflJd+8rphjyUVloutNgBjDeo78biMa/HQQrkro9LI/ZeJA3l/pNsa5Ik4pRlP9C+UqFPMKtvLIkFIMIknHHWJlyUVw+PM6fiiC0hd6qrGl35hD0WEiVELvDOa9juSin/97gXWho+XT+9zCIMHB46aoiEGq9aRVfLUSKHNQWgE7cejXZD3wljpK/DVfqMLIs6ML9NMkhcZ1V16oWoAnmSB7VmSIyIppof9YgemBSovdfgr7YnukV5h/Fji7m1vFWXyqxQGnndpx6F2pFitEOpHYZHAzmiEN5qJvoU7VAib+cbLpk7IBeDu9h4htgzhJRW/7AMsM4rQSQL3/rYkpoPtiRUTIJ+IRglbsihwsyAGGFU+9xoQL9FmrGr3EyAyyW8dfvtX3IEke7C6dFkduNFNlo2B6T7V0CbL6uACc3Wylcr+o/Ju9P0FmIPL0FRpBuro+OgF2L08lLgmdnIZvqQZ0cqPs0UzOw4jwCtcda4hMzCPrGRwPkDMmgOs8oQEp5AjO3h1e2/HTXZMi+T5upYrASRWGTe+lXwm7/9+Km+Gl/RNJsjpVpdEk3nL8ThVu3JWYZJFY/oaIV1QTgjyNalLp8wqMFJkXmstiyTCTNpPai8E32aMB69yyPSrU1PdaEutCv91NIQ3aUsFNaBiQ9V2XhSEdMsnOGErxqGlWzuG23ey3zWz/Pt3fqSQORdXk0uzKMV1zqRf+F4y/JO3XtsZH8wyxpY7expXhCAg/5vOXBTFlKDq3SpBjBf4Eta3rtdiu7irn4zC1BJgNeiJpV08wWElWHPpiZ4uE0AQrP+usnXzFHrJpxd41lkIdFZjXspv9v794PnJUViyYbUEPuETLPrCZdSvvPxVLdjz5avhzszkpN9qo81x+cRJA51IBYU9QUxohCveCwRHmy1O1BqC1ZlcbBcP4UULcZ2OZAYOcPwvjLCn+IVyMRJ/1hkqHs+inNQBP5AjnUXJHcq52RHNkqYZWz6W3lk6uarsRopK9yV2NXukONOEjSrbkDScFeLRPeGS0V19JC6+8PdqN4qPGxFZx27yC0JlYoH0XKayIjP9fO+fU6USQiZmPQ1W2U24SrLC5qxBKcn4PxVfA8ss2GVtwBHFMje6ZagMfejd+IGnJdkhyZQ3Hf+dodkB5sS/Cp93YKd6XQoq/eygjdfxJRLJ/ouTbyt3C5gcGPuMf5mM7b/pPoDsH1TRML/z/Vkfgnm9nZlvFDHedtqlSIgSbEIfBltksbMXA4qotaXTLZ+e3JNAhE4rrcNVkk6RqGw0Zczn4LmHFuMesPRD7Xc1vXmxk+RA+bUc5fDT0bRiiNVabzofGTuSRFFbIBIPogTezKcCnpfdl+avAVLO676ZZ5HBr0nbzL8pSELotDcbsQ2/fqV+jrepCRh654tkLopWGWYhoi6aZ5USX9rP3O5CMpX0BvXg726oW3NzViuc3A6XD0kEIkW/3IZa84yQTTuknARd93mquSSBluzU3Rdl+0pmjJL2H0vAs0QEfP5mc5n3wqrl7OsKQRzc8QrnHNx5vrybeiXEkc6oebXhWW1KungWzZSLhJ36F2Voq/3mvowBUw4d/emOhsZYm4ChgG/Y/assz889rYm0hkU32jjDOLw1VeC6QgBXkEeWRIwq55HY8rGQKs9O8fgPm8ZDqV5RKfTC93cx4IXCRFtPljGPC2tEy/PE1KfFFOA/chDVRcrIZNrx07San2JIRcXySmq66nuXtqXeb35nUFay+iSVjN5dOEhtkl0xVYuXbYllu+5flgRWTRFU2TKnbEJSVkA9SGvtfa+tJon1FAqOCETcv7IxcPljwJLj1mIYG0kFKduQNjF2mougFw8rFIKZrNkHdbpyd+T7RpO+gWd17lC+Na52wKEDkkpwWsco95U4Kl2td5gy0ntMrVsSs/m9jWYtggYsRNuZxisik0uiXHwXYYAjdCGUvCvOnayhtzVn7TSnWJXg783sDnIEzqNKIolRJ5hTwpTe/FrZvO4egS00tV8pb7eeY64CgFS1lpbnQ9aA1wx+nZFtXDvDODDnwitL6SX+Xa63An/C1ha7KVxGMtXiInzEYF7uLQikrxaTev2EJlICxnnLIY5YFnjktX+/ccERkxkI72W/8pC93WfiSBF/U+hjJ1oGIjYEp3Przstx2EsK5GstVdiGex84/SlHGKsV6bZ5LuDtfFKH0NIL7a4laYs7WVOgOnksr94+srgWgs8gr434MlKBnUbSQIShVwn4ZH798flwJa9MyvQOjOi2XlauQXZiBBEb0BKY+0XAHk8gMnaUHCA8M5VnieiCsZIgIsUs0IFLBxGLApZ/IvuMyGz7H4zXJbHVCLU84NelXtcVLnr17B82ExuVWlSo9hLEn/Xj5+PvDu/xRL4Iq5V5wQuYc/D/yXkBtFbLoUWeydVlvJo09ZeIamZM1W4ykuHtn6jR3teyfkAIMDMoBGDceBCGykyALtm0q/vWOZnRHSvtAfK+tzrQdPbWpbRicB1hShoEVQ9vMA6pWje/zkXOnE6BlxqEvR6Xpzkpq/+YlxlxZt6tiz4MrKDIm+mu00TUFFv6B9CbTTm6zWtlIjKm25g0I4Lrb84CM3/XEzHV9Vog/Y5WpRPLV4i7oTIPpGXv0coRtVXrrKH2giTJsKz40Gxz9LGHBsV1FC3F/3yaetDM4xdWVAs/cu1HopRirwhvhBmxANban0CsIMsMpJG/Qsd6kU5v3reew1g2SfDuy+6TSvLkH3eGkt5wZrJA9Qparz+xQFgOqp+qh8ieiQEbap+22itPLgf/8NaAZCsymVvhdlLVev/BYNNdLlI4b7ZtI0SJG4cUn+Ac88JiasGxBBud9dVTwQD9+jnZXI8Jsg5baY1PAJG0nuBBG09mFjs0elzH/4w+Tl5k/H4eoF005lsikofbJQeultQK8ALjOFqmH28hlH05a1rqftRI7NWHgcIxJE7WKQIO03DSjY6bwqic5h9wMOsir/1nmMoTb1jx0tPzB353aIAvrcSEh4FleFTpmLFWEWn1IIIvCAuWqPo+9nK2K0R6vTp7ENjOYuDavq+ECLO51T9P/YfSvkVpTDlMNjBk799QRzwGDy7/oZJiS9jwiYHxiQLpWEqcGAHnwYtVEpFujpYD0v92UyTD4D6F7tu1ro4ygSFjP9FlaaO3n7pf+b6gW8jFJh47oTFwBO6IVHSQQ+GDa+HRJZpJg3Lj8e1nCAhjW0k+cSZXb1/8nFtC+imxIqB8DyWCeiUsnADb/LGd8IhPEl3zHRzMBbPE5xoW8M1JXpmnmzgpqV3HMsyjwZmucMBluBHHQaAeHl4cb2f5v0vTxCKnYWlTAgHQEp0wkiRGAlQIUL+L2aXN9fMQc04G4dFxbZSUk0vCKkpQzDSrfaIckxhbpkF9d3s0wk/u6uy5StgeMeuzMUwjxSkLef+GqLhFt/aoR31ZXa+lDCyCVMADem/3Ip12lamwQb0TGMW6EArhJYIz+/ghlv8QcqADTrZV7a8sVqAMvAoSsU96pV2GEwcxRDtDMYGbl+XysNSeMBlw8ssZH991+m83JQITcl+89rs1KbmODC4MgrtV8Gb4Hy0inmQZhaPMu0qXRZ/ug+qYyWnWCVp/kXkabfVowyysBGib+g10kW99IdBlLs4w5u3SNpkgCAdZS/2m/vep//F6L+0n4DtQfmCZkLR85MW4NVoo4uzxPQKWKMQ66GGuHBifIVQOaeCJgKRq+dwChtkA1Iqu08OZffEUl3hA8NDueuZxRq3YV1UQJH3A0y+ZR7X3aht8/MiUGFZf5sM4hK3vmf7dyOpLOz5+Vckb+l4bsU9rG6IdQHP4MV/o7oX6JngdYnS7bil1e7ECDvkdBauJan48NU+p1IHE4NJGV1iaoNienZXoyrWJxXGEPznxwQM/PT5OjUrIwVoJT+bW+CRL1OjD2eJRpE3A86arco2pTDLsp1gBTUGm4AK9vozRT0oPs9X4ccyfAA/LledwO+NDruF/8e6xu7yu7izPK9dkt6xK0duGI72y/66cBVW2hxDo9ils3Lg+WmFFSHhalyzYpi24GifA28QicRfW55k9DBylOnTvTwGN28Ly9DOlcQH3fOlosQt5uK1nWlF5sORh/hAAkFIAitixVwzTTqtYk1BE4RqplnBZIObJzoTdLfl1U/03AqD4J0rnERn+1R+EsC6ECN0MAHiI7eXyXwb03ZrlpJkM3lC6p9GFoBiD4ooZ+Ik09KJAVmjcCjdaYBoSHgXjI/WhZfXrMl7CPCqrpQYul15icNqKGRBnBFnLqm8H7J4LAhRDp+3SLiMWpPCae59c4x+VIS+w3EsShQ7FI7ALgV+LUC6KTZy5OvUgkb2O9U3f3nC0iB2nocbuuZYP1opabzcLGzFrOm2KZKCfVDBm1S7gHHLt/9na0nH6XvAfC5/wWYDeBIyeBLYUDuAUhUd2afYdfSQecFwFsXNgdSxQy4Jnd3PJbp5eeqjFsn88P02ph5sQptVldEaxIZS58S4oe2mK7XHFYoJhNdP0YFAHxRn4HNoWhle4vOtUE/BVvmgZgnc98imcEn51UgOOELlKqxTuocvEzhINHd/SerStONU8kwGbdfMkQxHJ6Ks5EENWhGhqkXZ78jzCnh5rUpiVh9ZsitZw7y4azJxIy1XgCni29hUqoJk+zqZ4ikGs50a9r88TvziI17XrU4QxoJZlSIOjT2Ju0USwZOk+rfpc7bEznt7r9qkCKFRQYahEl5JOrnZJ0zD8jC5MjeTvw8P9CA+zxP3APEJ2zNa5c1hE64fqG0JxX5tmPjdF46b2zV1ekRJzm+gz9CetCPIIwny1fjFcvyP+e5SGY+jCRohkyCeXB4waH9y/CqV
Variant 1
DifficultyLevel
533
Question
Axe went jogging and stopped after 62 of a kilometre to take a rest.
Which of these represents where Axe stopped jogging?
Worked Solution
Each spacing is worth 61 km.

Question Type
Multiple Choice (One Answer)
Variables
| Variable name | Variable value |
| question | Axe went jogging and stopped after $\dfrac{2}{6}$ of a kilometre to take a rest.
Which of these represents where Axe stopped jogging? |
| workedSolution | Each spacing is worth $\dfrac{1}{6}$ km.
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2021/03/NAPX5-29-1-1.png 240 indent vpad |
| correctAnswer | sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2021/03/NAPX5-29-1-1.png 240 indent vpad
|
Answers
| Is Correct? | Answer |
| x | 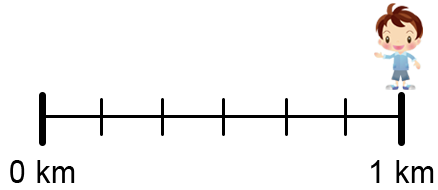 |
| x | 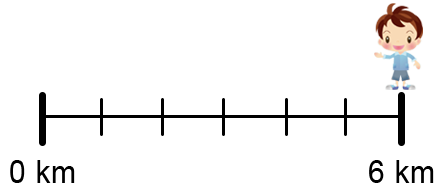 |
| ✓ |  |
| x |  |