20299

Question

The surface area (S\large S) of the prism below can be calculated by multiplying the perimeter of its face (p\large p) by its height (h\large h), and adding twice the area of its face (FF).



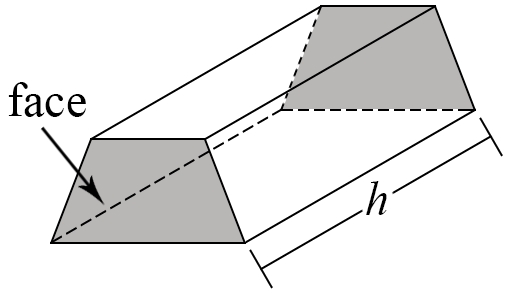
Which one of these formulas could be used for this calculation?

Worked Solution

{{{correctAnswer}}}

Variant 0

DifficultyLevel

558

Question

The surface area (S\large S) of the prism below can be calculated by multiplying the perimeter of its face (p\large p) by its height (h\large h), and adding twice the area of its face (FF).



Which one of these formulas could be used for this calculation?

Worked Solution

S=ph +S = \large p h\ + 2F2F

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
correctAnswer
$S = \large p h\ +$ $2F$

Answers

Is Correct?Answer
x

SS = 2ph2 \large p h × F\times \ F

x

S=ph +S = \large p h\ + FF

✓

S=ph +S = \large p h\ + 2F2F

x

S=2ph +S = 2 \large ph\ + 2F2F