60003

Question

{{{question}}}

Worked Solution

{{{workedSolution}}}

Variant 0

DifficultyLevel

548

Question

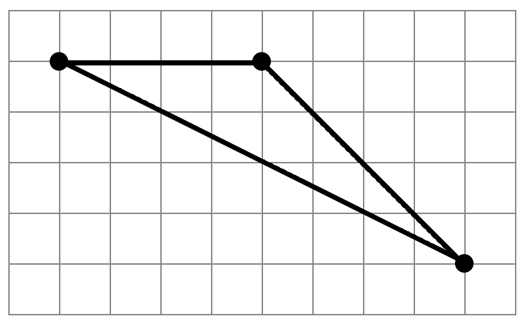
A triangle is drawn on grid paper.

What is the area of the triangle?

Worked Solution
Area = 12 ×base × height\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}
= 12 × 6 × 5\dfrac{1}{2}\ \times\ 6\ \times\ 5
= 15 squares

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
A triangle is drawn on grid paper. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2018/06/NAPX-J3-CA11_1.svg 220 indent3 vpad What is the area of the triangle?
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2018/06/NAPX-J3-CA11.svg 220 indent vpad
| | | | --------------------- | ------------------------------------------- | | Area | \= $\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}$ | | | \= $\dfrac{1}{2}\ \times\ 6\ \times\ 5$ | | | \= {{{correctAnswer}}} |
correctAnswer
15 squares

Answers

Is Correct?Answer
✓

15 squares

x

16 squares

x

18 squares

x

20 squares

Variant 1

DifficultyLevel

564

Question

A triangle is drawn on grid paper.

What is the area of the triangle?

Worked Solution
Area = 12 × base × height\dfrac{1}{2}\ \times\ \text{base}\ \times\ \text{height}
= 12 × 4 × 4\dfrac{1}{2}\ \times\ 4\ \times\ 4
= 8 squares

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
A triangle is drawn on grid paper. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2017/09/NAP-J1-CA11_1.png 300 indent3 vpad What is the area of the triangle?
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v1_ws.svg 300 indent vpad
| | | | --------------------- | -------------------------------------------- | | Area | = $\dfrac{1}{2}\ \times\ \text{base}\ \times\ \text{height}$ | | | = $\dfrac{1}{2}\ \times\ 4\ \times\ 4$ | | | = {{{correctAnswer}}} |
correctAnswer
8 squares

Answers

Is Correct?Answer
x

6 squares

✓

8 squares

x

12 squares

x

16 squares

Variant 2

DifficultyLevel

547

Question

A triangle is drawn on grid paper.

What is the area of the triangle?

Worked Solution
Area = 12 ×base × height\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}
= 12 × 10 × 7\dfrac{1}{2}\ \times\ 10\ \times\ 7
= 35 squares

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
A triangle is drawn on grid paper. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v2.svg 320 indent3 vpad What is the area of the triangle?
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v2_ws.svg 320 indent vpad
| | | | --------------------- | ------------------------------------------- | | Area | \= $\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}$ | | | \= $\dfrac{1}{2}\ \times\ 10\ \times\ 7$ | | | \= {{{correctAnswer}}} |
correctAnswer
35 squares

Answers

Is Correct?Answer
✓

35 squares

x

55 squares

x

70 squares

x

77 squares

Variant 3

DifficultyLevel

546

Question

A triangle is drawn on grid paper.

What is the area of the triangle?

Worked Solution
Area = 12 ×base × height\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}
= 12 × 6 × 5\dfrac{1}{2}\ \times\ 6\ \times\ 5
= 15 squares

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
A triangle is drawn on grid paper. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v3.svg 360 indent vpad What is the area of the triangle?
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v3_ws.svg 360 indent vpad
| | | | --------------------- | ------------------------------------------- | | Area | \= $\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}$ | | | \= $\dfrac{1}{2}\ \times\ 6\ \times\ 5$ | | | \= {{{correctAnswer}}} |
correctAnswer
15 squares

Answers

Is Correct?Answer
x

7.5 squares

x

12 squares

✓

15 squares

x

30 squares

Variant 4

DifficultyLevel

545

Question

A triangle is drawn on grid paper.

What is the area of the triangle?

Worked Solution
Area = 12 ×base × height\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}
= 12 × 3 × 5\dfrac{1}{2}\ \times\ 3\ \times\ 5
= 7.5 squares

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
A triangle is drawn on grid paper. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v4.svg 360 indent3 vpad What is the area of the triangle?
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v4_ws.svg 360 indent vpad
| | | | --------------------- | ------------------------------------------- | | Area | \= $\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}$ | | | \= $\dfrac{1}{2}\ \times\ 3\ \times\ 5$ | | | \= {{{correctAnswer}}} |
correctAnswer
7.5 squares

Answers

Is Correct?Answer
x

3.75 squares

x

4 squares

✓

7.5 squares

x

15 squares

Variant 5

DifficultyLevel

544

Question

A triangle is drawn on grid paper.

What is the area of the triangle?

Worked Solution
Area = 12 ×base × height\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}
= 12 × 2 × 4\dfrac{1}{2}\ \times\ 2\ \times\ 4
= 4 squares

Question Type

Multiple Choice (One Answer)

Variables

Variable nameVariable value
question
A triangle is drawn on grid paper. sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v5.svg 350 indent3 vpad What is the area of the triangle?
workedSolution
sm_img https://teacher.smartermaths.com.au/wp-content/uploads/2022/08/Measurement_60003_v5_ws.svg 350 indent vpad
| | | | --------------------- | ------------------------------------------- | | Area | \= $\dfrac{1}{2}\ \times \text{base}\ \times\ \text{height}$ | | | \= $\dfrac{1}{2}\ \times\ 2\ \times\ 4$ | | | \= {{{correctAnswer}}} |
correctAnswer
4 squares

Answers

Is Correct?Answer
x

2 squares

✓

4 squares

x

3 squares

x

8 squares

Tags